Vector Fields

Vector value functions $\ne$ vector fields
Bounded above for any solution $y$ $\mathrm{\exists }M\in \mathbb{R}\text{ such that }y(t)\le M\mathrm{\forall }t$

Let $M=y(0)$ since $y^{\prime }\in \{-2,0\}$ it is monotonic/non-increasing $⟹\mathrm{\forall }ty(t)\le y(0)$

1. Vector Field: A grid of arrows representing the field, with their tails anchored at points in space and directions/magnitudes defined by the vector field. Can be thought of as $(x,y)\mapsto \left[\begin{array}{c}x\\ y\end{array}\right]$

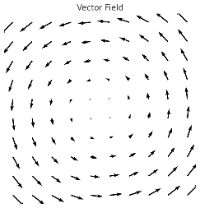
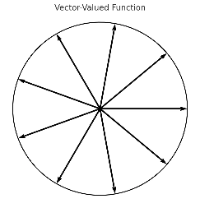
2. Vector-Valued Function: A set of vectors originating from the origin, with their tips tracing out a curve.
   

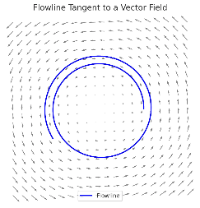
Flowline

if $F$ is a vector field and $c(t)$ is a flowline then $F(c(t))=c^{\prime }(t)$

Differential Operators

Gradient

$\mathrm{\nabla }$ is a mapping on a space of functions to real vector fields
$\mathrm{\nabla }=[\frac{\partial }{\partial x_1},\dots ,\frac{\partial }{\partial x_n}]$

if $\mathrm{\nabla }=\left[\begin{array}{c}\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}\end{array}\right]$ then we have:
$\mathrm{\nabla }:C^1({\mathbb{R}}^3)\to V({\mathbb{R}}^3,{\mathbb{R}}^3)$

Gradient Field

$f:{\mathbb{R}}^n\to {\mathbb{R}}^n$
is a gradient field if $\mathrm{\exists }F$ such that $f=\mathrm{\nabla }F$

Divergence

div($F$) := $\mathrm{\nabla }\cdot F$

Source

if div($F(x_0)$) > 0 then $x_0$ is a source

Sink

if div($F(x_0)$) < 0 then $x_0$ is a sink

Curl

cur($F$) = $\mathrm{\nabla }\times F$
and = 0 if $F$ is a gradient vector field

Conservative Vector Field

$F:{\mathbb{R}}^3\to {\mathbb{R}}^3$ is a conservative vector field if any:

1. $F=(\mathrm{\nabla }f{)}^T$
2. ${\int }_{c}ds$
3. ${\int }_{c_1}F\cdot ds={\int }_{c_2}dxF\cdot ds$ where $c_1\text{ and }{c}_2$ are curves with the same end points
4. curl(F) = 0

There exist both:

A scalar potential g such that $\mathbf{F}=\mathrm{\nabla }$ g, and
A vector potential $\mathbf{G}$ such that $\mathbf{F}=\mathrm{\nabla }\times \mathbf{G}$.

if

Curl-free ($\mathrm{\nabla }\times \mathbf{F}=0$), so it has a scalar potential g.
Divergence-free ($\mathrm{\nabla }\cdot \mathbf{F}=0$), so it has a vector potential $\mathbf{G}$.