Green's Theorem

Green's Theorem for Elementary Regions

Lemma 1

Let $D \subset R^{2}$ be y-simple and $P : D \to R$ be a $C^{1}$ function on $D$ and $\partial D$ is a $C^{1}$ path

\int_{\partial D^{+}} P d x = - \int \int_{D} \frac{\partial P}{\partial y} d A

where + is counter-clockwise

pf:
Say $D$ is like

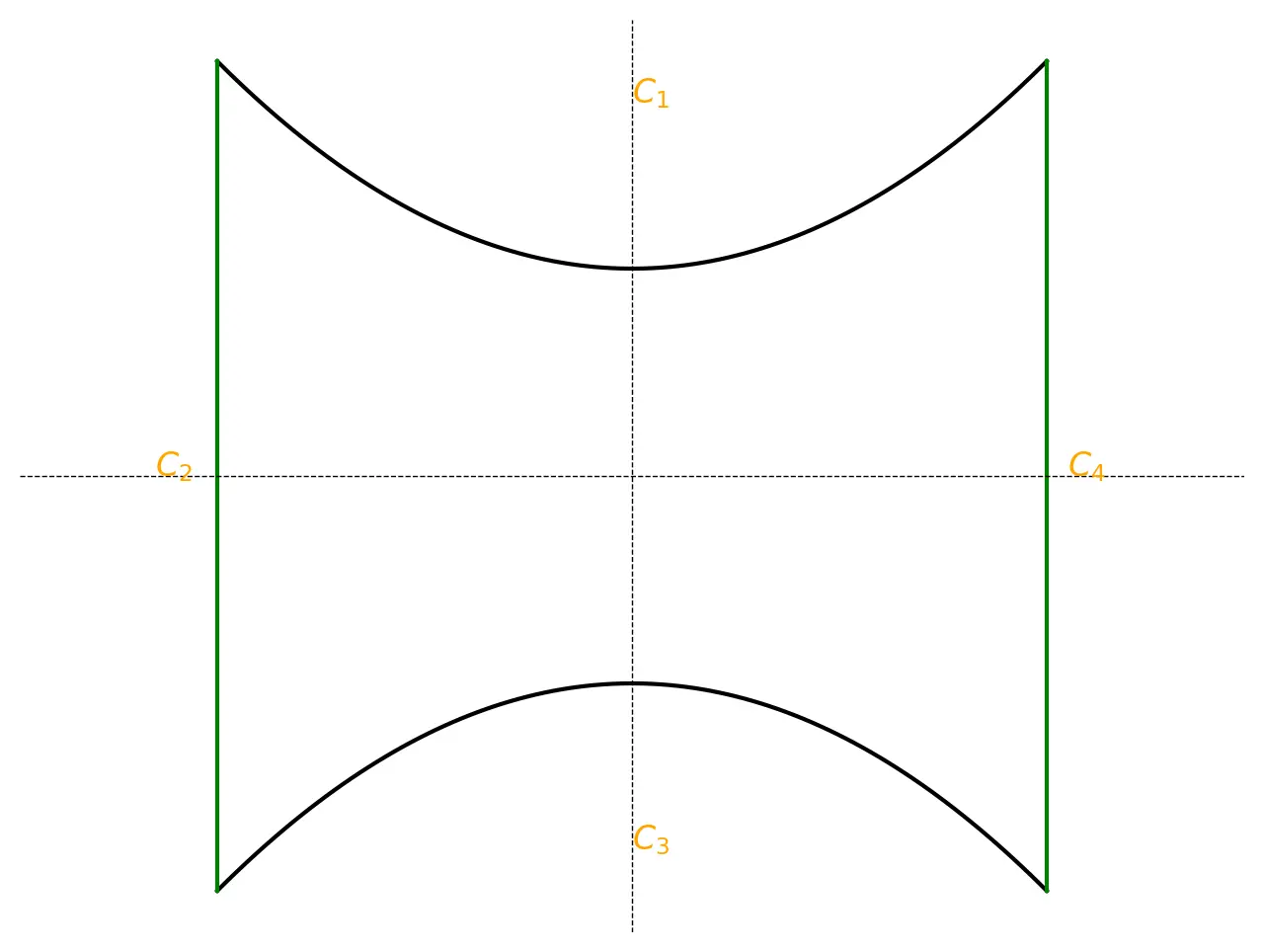
Pasted image 20241213150401.webp|422

\begin{aligned} - \int \int_{D} \frac{\partial P}{\partial y} d A & = - \int_{a}^{b} \int_{ϕ_{1} (x)}^{ϕ_{2} (x)} \frac{\partial P}{\partial y} d y d x \\ = - \int_{a}^{b} (P (x, ϕ_{2} (x)) - P (x, ϕ_{1} (x))) d x \\ = \int_{a}^{b} (P (x, ϕ_{1} (x)) - P (x, ϕ_{2} (x))) d x \\ = \int_{c_{3}} P d x + \int_{c_{1}} P d x \\ = \int_{\partial D} P d x \end{aligned}

The same follows for x-simple regions

\int_{\partial D^{+}} Q d y = \int \int_{D} \frac{\partial Q}{\partial x} d A

Green's theorem

Assume $D$ is a closed simple region
and $P : D \to R$ and $Q : D \to R$ are $C^{1}$

\int_{\partial D^{+}} P d x + Q d y = \int \int_{D} (\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}) d A

We can think of a vector field $F = [P, Q]$

This is equivalent to using curl

$since cur F = | \begin{matrix} i & j & k \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial x} & \frac{\partial}{\partial z} \\ P & Q & 0 \end{matrix} | = [\begin{matrix} 0 \\ 0 \\ \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \end{matrix}]$

So we have

\int_{\partial D^{+}} F \cdot d s = \int \int_{D} (cur F) \cdot k d A

where $k = [0, 0, 1]^{T}$

Flux and Green's theorem

If $c (t)$ is a $C^{1}$ curve in the form of $c (t) = [\begin{matrix} x (t) \\ y (t) \end{matrix}]$

then we can compute the unit normal at $t$ as:

n (t) = \frac{1}{| | c^{'} (t) | |} [\begin{matrix} y^{'} (t) \\ - x^{'} (t) \end{matrix}]

where

n (t) \cdot T (t) = 0

(see unit tangent)
Let $c : [0, T] \to R^{2}$ be a parameterization of $\partial D^{+}$

\begin{matrix} \int_{\partial D} F \cdot n d s = \int_{0}^{T} F (c (t)) \cdot n \cdot | | c^{'} (t) | | d t = \int_{0}^{T} (P (c (t)) y^{'} (t) - Q (c (t)) x^{'} (t)) d t = \int_{\partial D^{+}} P d y - Q d x \\ = \int \int_{D} (\frac{\partial Q}{\partial y} + \frac{\partial P}{\partial x}) d A \end{matrix}

Using divergence we can write this as:

\int_{\partial D} F \cdot n d s = \int \int_{D} div F d A

Area of a Simple Region

A (D) = \frac{1}{2} \int_{\partial D^{+}} x d y - y d x = \frac{1}{2} \int \int_{D} \frac{\partial x}{\partial x} - \frac{\partial (- y)}{\partial y} d A = \int \int_{D} 1 d A