2. K-nn Regression

K-nn method (Regression)

The best possible value for $\hat{f} (x_{0})$ is

\hat{f} (x_{0}) = E [Y_{0}] = f (x_{0}) .

Given data $(x_{1}, Y_{1}), \dots, (x_{n}, Y_{n})$ , how do we learn/estimate $f (x_{0})$ ?

First: assume $x_{1}, \dots, x_{n}$ take only values $0$ or $1$ and $x_{0} = 0$ .
A natural approach:

\hat{f} (0) = Average (Y_{i} : x_{i} = 0) = \frac{\sum_{i = 1}^{n} Y_{i} I {x_{i} = 0}}{\sum_{i = 1}^{n} I {x_{i} = 0}}

Here,

I {x_{i} = 0} = {\begin{cases} 1, & if x_{i} = 0, \\ 0, & otherwise . \end{cases}

This works in data sets where $x_{1}, \dots, x_{n}$ take few distinct values and we are interested in predicting outcome for one of those values.

Idea: instead of requiring $x_{i} = x_{0}$ take $K$ of the ‘closest’ $x_{i}$ .
K-nn (K nearest neighbours) method:

\hat{f} (x_{0}) = \frac{\sum_{i = 1}^{n} Y_{i} I {x_{i} among closest K to x_{0}}}{K}

Bias-Variance

Variance

$Y_{i} = f (x_{i}) + ε_{i}$ , $ε_{i}$ i.i.d. with $E [ε_{i}] = 0$ , $Var (ε_{i}) = σ^{2}$ , $x_{i}$ fixed, $\hat{f} (x_{0})$ K-nn estimator.
Then, provided $K$ closest points $x_{i}$ to $x_{0}$ are unique:

Var [\hat{f} (x_{0})] = \frac{σ^{2}}{K} .

Derivation

\begin{array}{r} I_{i} = I {x_{i} among k closest to x_{i}} \end{array}

\begin{aligned} V a r (\frac{1}{k} \sum_{}^{} I_{i} Y_{i}) & \overset{i n d .}{=} (\frac{1}{K^{2}}) \sum_{}^{} V a r (I_{i} Y_{i}) \\ = \frac{1}{K^{2}} \underset{―}{\sum_{}^{} (I_{i}} \cdot \underset{σ^{2}}{\underset{⏟}{V a r (Y_{i})}}) \\ = \frac{1}{K^{2}} K σ^{2} \\ = \frac{1}{K} σ^{2} \end{aligned}

Bias

For simplicity: $x_{i} = i / n$ , $i = 1, \dots, n$ ,
$f : [0, 1] \to R$ two times continuously differentiable
$K = 2 ℓ + 1$
$x_{0} = j / n$ with $ℓ < j < n - ℓ$ .
Then:

E [\hat{f} (x_{0})] = \frac{1}{K} \sum_{u = - ℓ}^{ℓ} f (\frac{j + u}{n}) \approx f (x_{0}) + \frac{1}{24} f^{″} (x_{0}) {(\frac{K}{n})}^{2} + r_{K, n},

where $r_{K, n}$ is a remainder term, 'small' under suitable conditions.

Variance decreases as $K$ increases
Approximate squared bias increases as $K$ increases
To get a good MSE we have to balance bias and variance. This is called bias-variance trade-off.

Remark: if we let $ℓ = ℓ_{n}$ with $ℓ_{n} / n \to 0$ in the analysis above, this would be Asymptotic Statistics.

Derivation

K nearest neighbours

\frac{j - ℓ}{n}, \frac{j - ℓ + 1}{n}, \dots, \frac{j}{n}, \frac{j + 1}{n}, \dots, \frac{j + ℓ}{n}

\begin{aligned} E [\frac{1}{k} \sum_{i = 1}^{n} I_{i} Y_{i}] & = \frac{1}{K} \sum_{u = - ℓ}^{ℓ} E [Y_{j + u}] \\ I_{i} = 1 if i = j - ℓ, j - ℓ + 1, \dots, j + ℓ \\ = \frac{1}{K} \sum_{u = - ℓ}^{ℓ} f (\frac{j + u}{n}) \\ = \frac{1}{K} \sum_{u = ℓ}^{ℓ} (f (\frac{j}{n}) + \frac{u}{n} f^{'} (\frac{j}{n}) + \frac{1}{2} {(\frac{u}{n})}^{2} f^{″} (\frac{j}{n}) + \dots) \\ = \underset{f (x_{0})}{\underset{⏟}{\frac{1}{K} \sum_{u = - ℓ}^{ℓ} f (\frac{j}{n})}} + \underset{0}{\underset{⏟}{\frac{u}{n} \frac{1}{K} \sum_{u = - ℓ}^{ℓ} f^{'} (\frac{j}{n})}} + \underset{\frac{1}{2} \frac{1}{K} f^{″} (x_{0}) \sum_{u = - ℓ}^{ℓ} u^{2} / n^{2}}{\underset{⏟}{\frac{1}{2} \frac{1}{K} \sum_{u = - ℓ}^{ℓ} {(\frac{u}{n})}^{2} f^{″} (\frac{j}{n})}} + \frac{1}{K} remainder \end{aligned}

Validation

M S E_{t r a i n} = \frac{1}{n} \sum_{}^{} (\hat{f} (x_{i}) - Y_{i})^{2}

(x_{1}, Y_{1}), \dots, (x_{n}, Y_{n})

Should instead use a test set

Test Error

Population level quantity at a fixed value of predictor $x_{0}$ : for $Y_{0}$ new data point that is independent of $\hat{f} (x_{0})$

E [(\hat{f} (x_{0}) - Y_{0})^{2}] .

Population level quantity across a range of predictors: if $(x_{1}^{t e}, Y_{1}^{t e}), \dots, (x_{N}^{t e}, Y_{N}^{t e})$ is independent of $\hat{f}$ , average value of expected MSE

\frac{1}{N} \sum_{i = 1}^{N} E [(\hat{f} (x_{i}^{t e}) - Y_{i}^{t e})^{2}] .

If we had an additional sample, called test sample, $(x_{1}^{t e}, Y_{1}^{t e}), \dots, (x_{N}^{t e}, Y_{N}^{t e})$ which was not used to build $\hat{f}$ , we could try to approximate this error by

M S E_{t e s t} = \frac{1}{N} \sum_{i = 1}^{N} (\hat{f} (x_{i}^{t e}) - Y_{i}^{t e})^{2} .

$M S E_{t e s t}$ should converge to the population level
Not really WLLN since $\hat{f}$ relies on the other observations and both contain $N$ .

So we split into testing and validating but we have two issue:

split is random so our model might depend on the split
Splitting in half might give the wrong bias variance trade off, normally more data means less variance

V a r (\hat{f}) = \frac{σ^{2}}{K}

bias (\hat{f}) \approx c \cdot {(\frac{K}{n})}^{2}

Improving Cross-Validation

Average validation error over several random splits and/or use a larger portion of the data for learning and smaller for validation

L-fold Cross-Validation

Let $K = {k_{1}, \dots, k_{C}}$ denote the set of candidate values for $k$ in k-nn, i.e. we want to select the best one (in terms of test error) of those values.

Divide data into $L$ disjoint parts (folds) of roughly equal size. Call folds $S_{1}, \dots, S_{L}$ .
For $ℓ = 1, \dots, L$ , $k \in K$ , compute the k-nn estimator based on data
${(x_{i}, Y_{i}) : i \notin S_{ℓ}}$ (data not in fold $S_{ℓ}$ ).
Call resulting estimator ${\hat{f}}_{ℓ, k}, k \in K$ .
Compute test error on the $ℓ$ 'th fold

e_{ℓ} (k) = \sum_{i \in S_{ℓ}} ({\hat{f}}_{ℓ, k} (x_{i}) - Y_{i})^{2} .

The selected $k$ is the value with the smallest resulting error $\sum_{ℓ = 1}^{L} e_{ℓ} (k)$ over $k \in K$ , or

k = \arg min_{k \in K} \sum_{ℓ = 1}^{L} e_{ℓ} (k) .

{\hat{f}}_{1}, k is trained on the the other sets then applied on set 1

Standard Error Rule

For each value of $k$ , K-fold cross-validation returns estimated errors on each of the $K$ folds.
Call those errors $e_{1} (k), \dots, e_{K} (k)$ .

Those errors $e_{1} (k), \dots, e_{K} (k)$ are random variables (random splits, random data, ...).

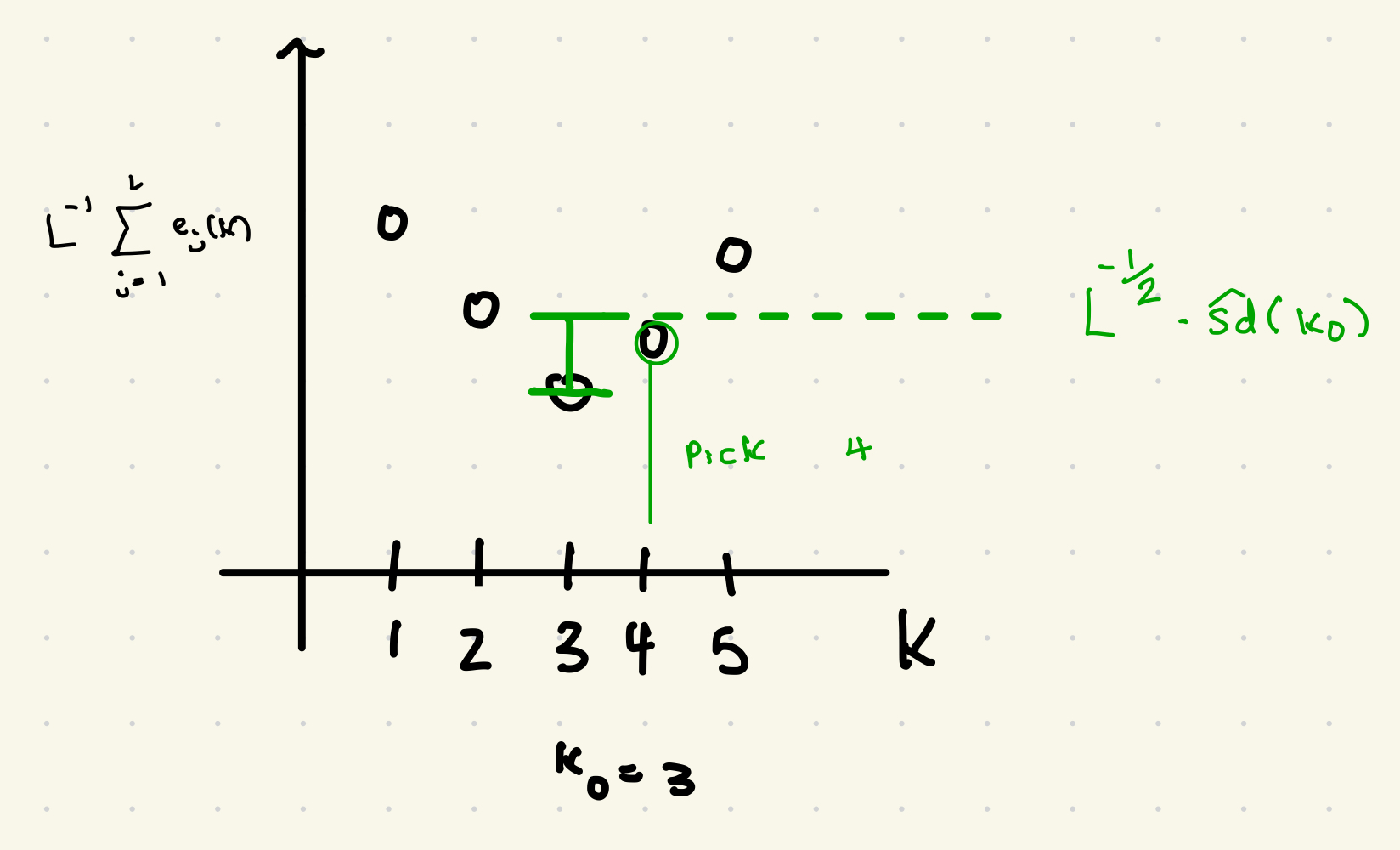
To reduce noise in model selection, and to select simpler models, one can use the one standard error rule.

For each $k \in K$ and each $ℓ = 1, \dots, L$ compute $e_{ℓ} (k)$ as in L-fold cross-validation.
Find $k_{0}$ which minimizes
$L^{- 1} \sum_{j = 1}^{L} e_{j} (k) .$
Compute $\hat{s d} (k_{0})$ , the sample standard deviation of $e_{1} (k_{0}), \dots, e_{L} (k_{0})$ .
Select the largest $k^{*}$ among those $k$ which satisfy
$L^{- 1} \sum_{j = 1}^{L} e_{j} (k) \leq L^{- 1} \sum_{j = 1}^{L} e_{j} (k_{0}) + \underset{estimate of sd of sample mean}{\underset{⏟}{L^{- 1 / 2} \hat{s d} (k_{0})}}$

Will tend to select simpler models than classical cross-validation (never selects more complicated models), i.e. larger $k$ for k-nn.
Good for building models that are more interpretable.
Recommended in textbook and other places, but not universally accepted.
No clear theoretical justification.

IMG_F06955603B1A-1.jpeg|384x233

Model Assessment

Divide into training and testing
Use training set to to fit candidates models. This includes tuning parameters with cross-validation
Use the final models to predict data in the test set and compute test error

Set aside 20%-30% of data for test

Drawbacks of K-nn Regression

Curse of dimensionality: does not work when there are many predictors, especially
of some of those predictors are not important.

Difficult to work with qualitative predictors (student status, color of a car etc).

Resulting model not very interpretable