1.2 First-Order Linear Equations

Constant Coefficient Equation

a u_{x} + b u_{y} = 0

where $a$ and $b$ are both constants not both zero

Geometric Method

We can think of $a u_{x} + b u_{y}$ as the directional derivative of the vector $V = a \hat{i} + b \hat{j} = (a, b)$ , $\nabla u \cdot V = 0$

Note that $(b, - a)$ is orthogonal to $V$ so therefore the lines parallel to $V$ have the form $b x - a y = constant.$ These are our characteristic lines.

A curve with tangent parallel to $V$ satisfies:

\frac{d y}{d x} = \frac{b}{a}

Solve this differential equation:

d y = \frac{b}{a} d x ⟹ y = \frac{b}{a} x + C

where C is an arbitrary constant.

Multiply through by a to clear the fraction:

a y = b x + a C ⟹ b x - a y = constant

We are essentially moving the same initial state across other initial conditions where the solution must have a constant value.

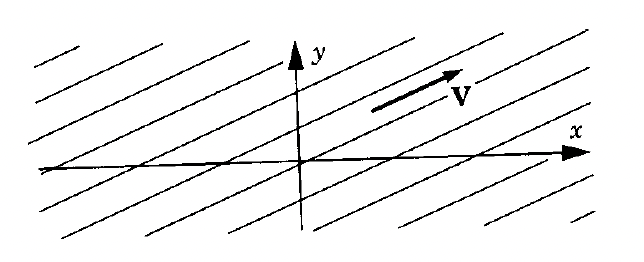
So along these lines $u$ has some constant value $F (C) = F (b x - a y)$
Let $u (x, y) = F (b x - a y)$ .

Compute:

u_{x} = F^{'} (b x - a y) \cdot b, u_{y} = F^{'} (b x - a y) \cdot (- a)

Plug into PDE:

a u_{x} + b u_{y} = a [b F^{'}] + b [- a F^{'}] = (a b - a b) F^{'} = 0

Coordinate Method

We employ a change of variables:

x^{'} = a x + b y, and y^{'} = a x - b y

\begin{aligned} u_{x} = \frac{d u}{d x} & = \frac{\partial u}{\partial x^{'}} \frac{\partial x^{'}}{\partial x} + \frac{\partial u}{\partial y^{'}} \frac{\partial y^{'}}{\partial x} \\ = a u_{x^{'}} + b u_{y^{'}} \\ u_{y} = \frac{d u}{d y} & = \frac{\partial u}{\partial y^{'}} \frac{\partial y^{'}}{\partial y} + \frac{\partial u}{\partial y^{'}} \frac{\partial y^{'}}{\partial y} \\ = b u_{x^{'}} - a u_{y^{'}} \end{aligned}

so $a u_{x} + b u_{x} = (a^{2} + b^{2}) u_{x^{'}} = 0, ⟹ u_{x^{'}} = 0 ⟹ u = f (y^{'})$

Variable Coefficient

u_{x} + y u_{y} = 0

We have $\nabla u \cdot (1, y) = 0$
or a chain rule where:

\begin{aligned} \frac{d y / d t}{d x / d t} & = \frac{y}{1} \\ \frac{d y}{d x} & = \frac{y}{1} \end{aligned}

This ODE has the solution

\begin{aligned} y & = C e^{x} ⟹ C = e^{- x} y \\ u (x, y) & = f (e^{- x} y) \end{aligned}