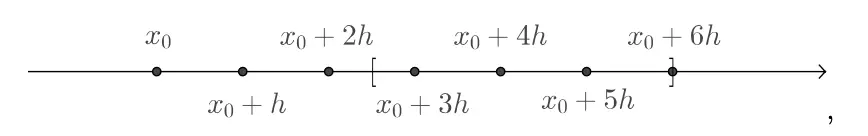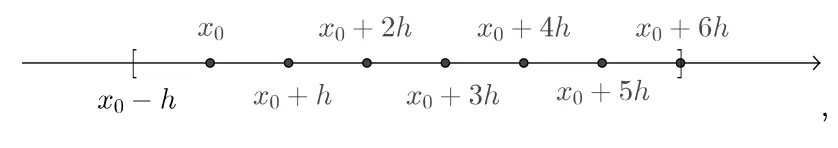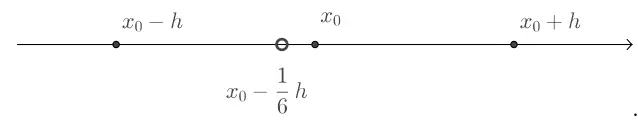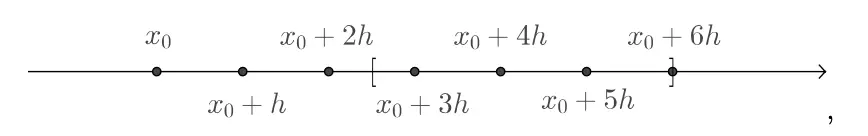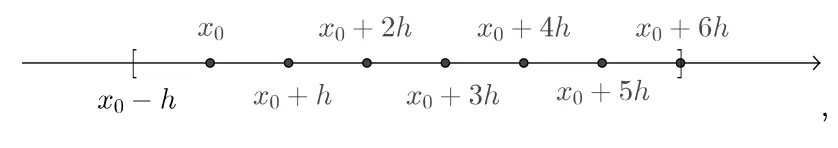4.1 Rudiments of Numerical Calculus

In 3.2 Lagrange Polynomials and 3.3 Newton Polynomials, we labelled the nodes of an interpolating function $x_0,x_1,\dots ,x_n$. It will be beneficial to begin calling them $x_0+{\theta }_{0}h,x_0+{\theta }_{1}h,\dots ,x_0+{\theta }_{n}h$ instead.

To see how this helps with the analysis, consider the degree at most 2 interpolating polynomial of $f$ with nodes

3.2 Lagrange Polynomials gives us:

but with the new notation, we replace $x_0$ by $x_0+{\theta }_{0}h$, $x_1$ by $x_0+{\theta }_{1}h$, $x_2$ by $x_0+{\theta }_{2}h$, and $x$ by $x_0+\theta h$, giving us

Stencils

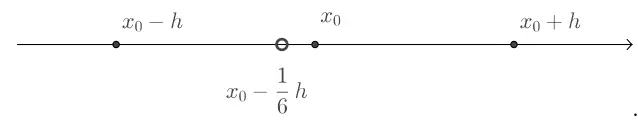
Not Evenly Spaced

Deriving $P_2(x_0)$ gives us:

Derivatives

Example: Want $P_2^{\prime }(x_0-\frac{1}{6}h)$
Over:

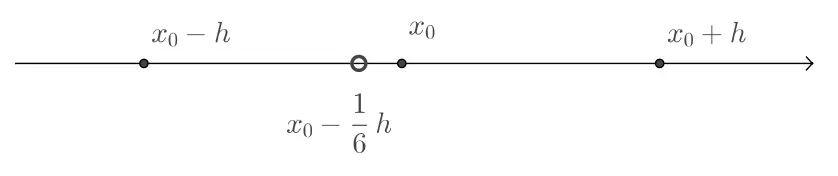
We can think of $x$ as a function of $\theta$ where $x=x_0+h\theta$, so $\frac{d}{d\theta }x=h$
Using chain rule $\frac{d}{d\theta }{P}_2(\theta )=\frac{d}{dx}{P}_2(x)\cdot \frac{d}{d\theta }x=h\cdot \frac{d}{dx}{P}_2(x)$
$⟹$

Based on the stencil ${\theta }_0=-1,{\theta }_1=0,{\theta }_2=1,\theta =-\frac{1}{6}$

If we did $x_0$:

Integrals