5.2 Derivatives and IVT
only works if x is an interior point
Derivative
Then is differentiable at if
Say
Example
,
If
if
Example
at 0
()
Example
Differentiable but is not continuous
For
apparently
apparently
At
Lemma: Differentiable then Continuous
If is differentiable at then is continuous at
Proof
Since is diff. at ,
So it is continuous
Lemma: Differentiable then Lipschitz
If is differentiable at then is locally Lipschitz
for all
Thm: Rademacher
Lipschitz functions are differentiable everywhere except on a "small set"
Algebraic Properties:
differentiable at
i)
ii)
iii)
iv)
v) , then
Thm: Fermat Interior Extremum
is diff. at
If has a local max or min at then
Proof
Assume is a local max.
Let and so for
Since is the local max there exists some so that:
Set For and
Since is differentiable at
For and
For and
Thm: Darboux
is differentiable on and then there exists some where
Proof
Let on .
is differentiable on with . So .
and are not minima and by EVT it must be the case then that there's a such that
Example
Is there a ? No will violate Darboux
5.3 Mean Value Theorem
Thm: Rolle's Theorem
Let be continuous on and differentiable on . If then there exists with
Proof
since is continuous on then there exists
Case 1: ,
Case 2: Set
Case 3: Neither or , but therefore is constant on so
Thm: Mean Value
If is continuous on and differentiable on then there exists a point where
Proof
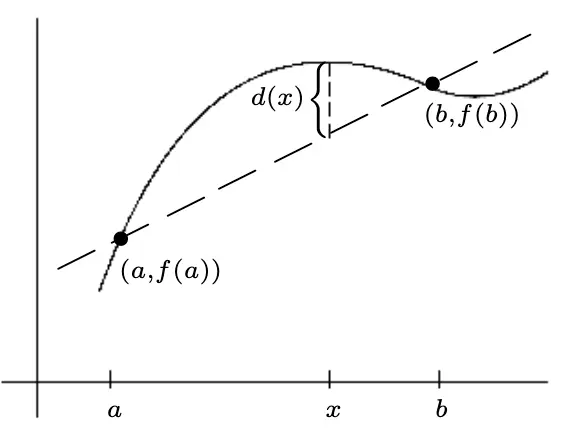
is continuous on , differentiable on and we have the system of equations:
By Rolle's Theorem there exists a point where
Thm: Cauchy Mean Value
are continuous on and differentiable on . Then there exists with
If , then:
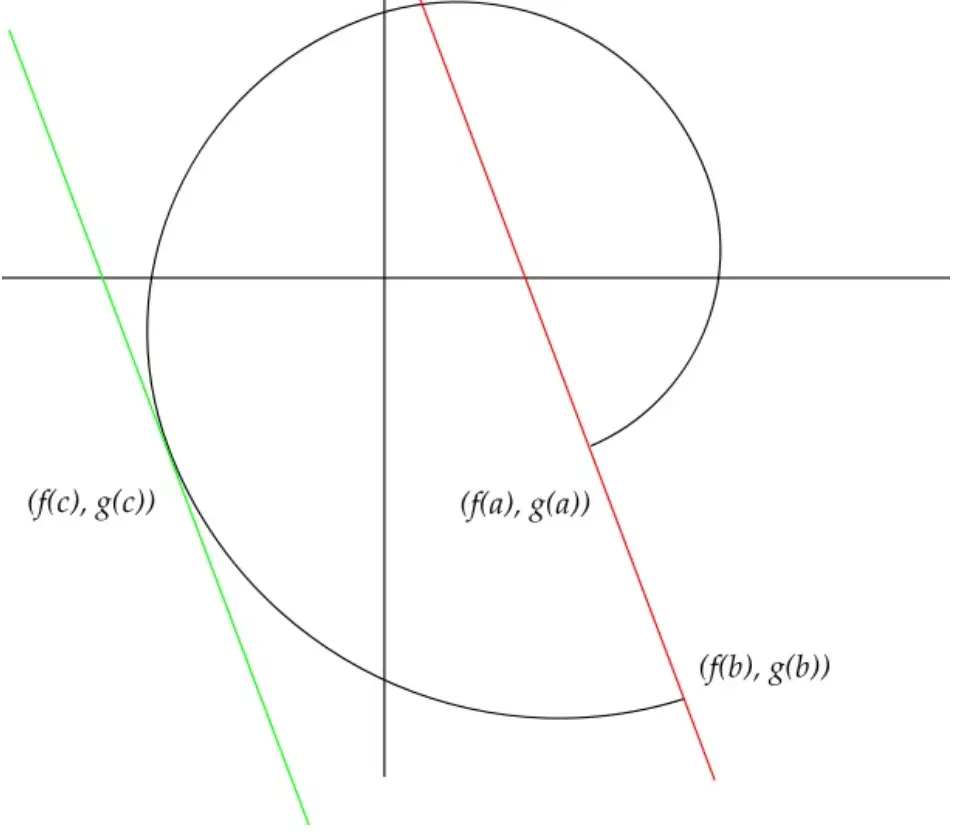
Thm L'Hospitals 0/0
differentiable and and
For all . Assume
If then
Assume and are differentiable on and that for all .If (or ), then

